XOR 연산은 입력값이 같지 않으면 1을 출력합니다. 이는 두 입력 중 하나만이 배타적으로 참일 경우에만 일어납니다. 이 연산은 더해서 mod 2 를 구하는 것의 결과와 동일합니다. 다음은 진리표입니다:

0 XOR 0 = 0

0 XOR 1 = 1

1 XOR 0 = 1

1 XOR 1 = 0

1. Multi-set(or Bag)
   • referred to as bag
   • set in which each element may occur multiple times
   • B(D) = D -> N ( finite domain D)
   • x ∈ B(D)
   • the difference(x\y) = A-(A ∩ B)
2. Firing Rule -a notation for input(output) places(transitions)
   • N = (P,T,F) / P,T 는 SET이다
   • P ∪ T are called nodes

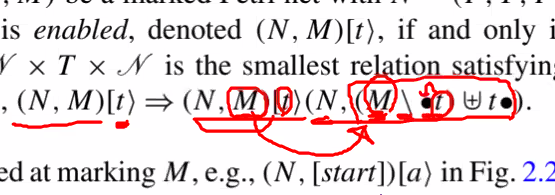
4.Labeled Petri net

• tuple N = (P,T,F,A,l)
• A는 activity labels(작업 표지), l는 labeling function(표지 함수)
• (P,T,F) is a Petri net

5.Reachability Graph

• TS =(S,A’,T’)

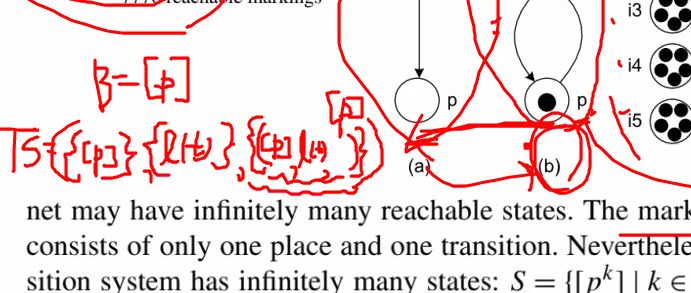
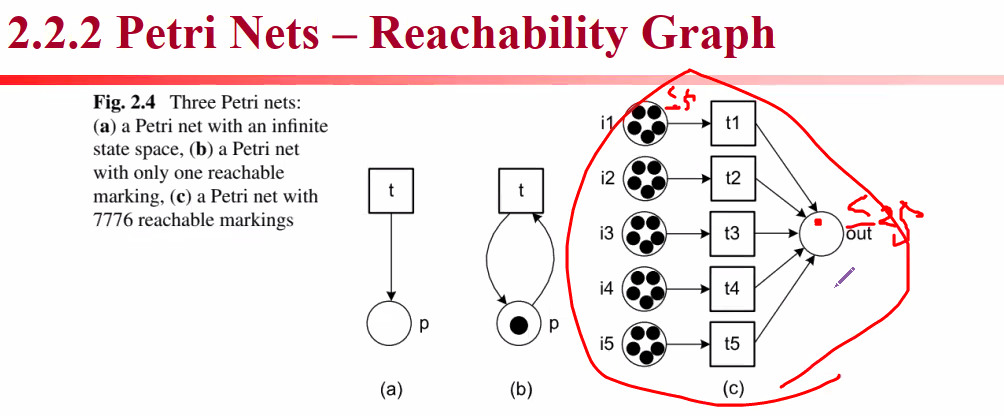
-three petri nets

(a) a petri net with an infinite state space / unbound(제한되지 않는) 페트리넷

(b) a petri net with only one reachable marking / 제한되어 있다 (bounded)

(c) a petri net with 7776 reachable marking / 제한되어 있다 (bounded)

(a) 표기법 => N=({p},{t},{(t,p)}) / M= (b) 표기법 => N=({p},{t},{(t,p)}) / M=p

6.Marked Petri net

• (N,Mo) is k-bounded(k-제한) if no place ever holds more that ktokens.
• a marked Petri net is safe if and only if it is l-bounded.
• A marked Petri net(N,Mo) is deadlock free if at every reachable marking at least one transition is enabled.

사진 출처 -경희대 정재윤 교수님