Airbnb-price-prediction-model을 하기위해서는 KNeighborsRegressor을 제대로 알고 넘어가자~!!

Airbnb-price-prediction-model

sklearn.neighbors.KNeighborsRegressor

Airbnb-price-prediction-model을 하기위해서는 KNeighborsRegressor을 제대로 알고 넘어가자~!! __________________________ 목표는 훈련 세트에서 가장 가까운 이웃과 관련된 목표의 로컬 보간에 의해 예측된다.

Parameters

n_neighborsint, default=5

kneighbors 쿼리 에 기본적으로 사용할 이웃 수입니다 .

weights{‘uniform’, ‘distance’} or callable, default=’uniform’

예측에 사용되는 가중치 함수. 가능한 값 :

‘균일 한’: 균일 한 가중치. 각 이웃의 모든 포인트는 동일하게 가중치가 부여됩니다.
‘distance’: 거리의 역으로 가중치 포인트. 이 경우 쿼리 포인트의 가까운 이웃이 먼 이웃보다 더 큰 영향을받습니다.
[callable] : 거리 배열을 허용하고 가중치를 포함하는 동일한 모양의 배열을 반환하는 사용자 정의 함수입니다.

기본적으로 균일 한 가중치가 사용됩니다.

algorithm{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’

가장 가까운 이웃을 계산하는 데 사용되는 알고리즘 :

‘ball_tree’는 BallTree를 사용 BallTree
‘kd_tree’는 KDTree를 사용 KDTree
‘brute’는 무차별 대입 검색을 사용합니다.
‘auto’는 fit 메서드에 전달 된 값을 기반으로 가장 적합한 알고리즘을 결정하려고 시도합니다 .

참고 : 스파 스 입력에 피팅하면 무차별 대입을 사용하여이 매개 변수 설정이 무시됩니다.

leaf_sizeint, default=30

잎 크기는 BallTree 또는 KDTree로 전달되었습니다. 이는 트리 저장에 필요한 메모리뿐만 아니라 구성 및 쿼리 속도에 영향을 줄 수 있습니다. 최적의 값은 문제의 특성에 따라 다릅니다.

pint, default=2

Minkowski 지표의 전력 매개 변수입니다. p = 1 인 경우 manhattan_distance (l1) 및 euclidean_distance (l2)를 p = 2로 사용하는 것과 같습니다. 임의의 p의 경우 minkowski_distance (l_p)가 사용됩니다.

metricstr or callable, default=’minkowski’

나무에 사용할 거리 측정법입니다. 기본 메트릭은 minkowski이고 p = 2 인 경우 표준 유클리드 메트릭과 동일합니다. 사용 가능한 메트릭 목록은 DistanceMetric 설명서를 참조하십시오 . 메트릭이 “미리 계산 된”경우 X는 거리 행렬로 간주되며 적합하는 동안 정사각형이어야합니다. X는 희소 그래프 일 수 있으며 ,이 경우 “0이 아닌”요소 만 인접 요소로 간주 될 수 있습니다.

metric_paramsdict, default=None

메트릭 함수에 대한 추가 키워드 인수

n_jobsint, default=None

이웃 검색을 위해 실행할 병렬 작업 수입니다. None 은 joblib.parallel_backend 컨텍스트가 아니면 1을 의미 합니다. -1 은 모든 프로세서를 사용함을 의미합니다. 자세한 내용은 용어집 을 참조하십시오. fit 방법에 영향을주지 않습니다 .

Attributes

effective_metric_str or callable

사용할 거리 측정법입니다. 그것과 동일 할 것이다 metric 등의 파라미터 또는 동의어 ‘유클리드’만약 metric ‘민코프 스키’와, 파라미터 세트 p 2 파라미터 세트.

effective_metric_params_dict

메트릭 함수에 대한 추가 키워드 인수입니다. 대부분의 메트릭은 metric_params 매개 변수 와 동일 하지만 , effective_metric_ 속성이 ‘minkowski’로 설정된 경우 p 매개 변수 값 도 포함 할 수 있습니다 .

n_samples_fit_int

피팅 된 데이터의 샘플 수입니다.

X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
neigh = KNeighborsRegressor(n_neighbors=2)
neigh.fit(X, y)
KNeighborsRegressor(...)
print(neigh.predict([[1.5]]))

[0.5]

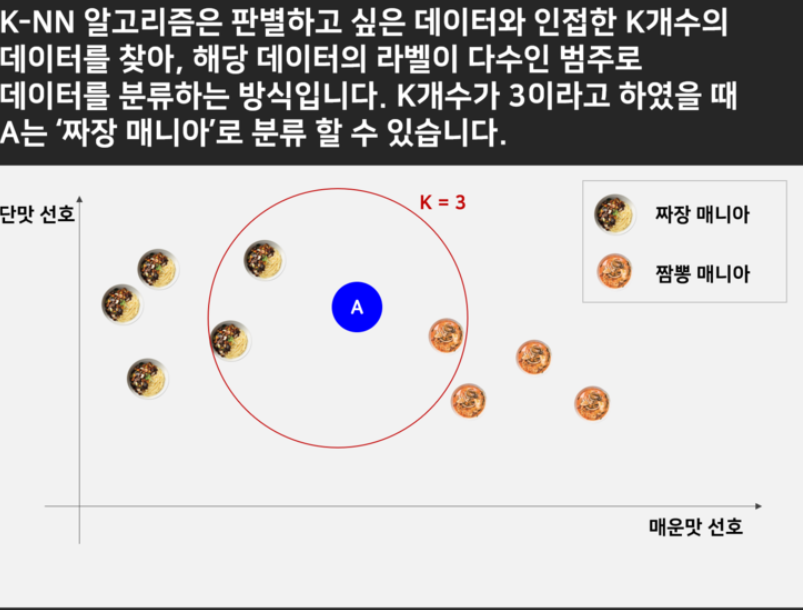
KNN 알고리즘 개념 쉽게 설명

KNN은 지도학습에 한 종류로 거리기반 분류분석 모델이라고 할 수 있다. 거리기반으로 분류를 하는 클러스터링과 유사한 개념이나 , 기존 관측치의 Y값이 존재한다는 점에서 비지도학습에 해당하는 클러스터링과 차이가 있다
유클리디안 거리 계산법을 사용함
이미지 처리,영상에서 글자 인식,얼굴 인식, 영화나 음악, 상품 추천에 대한 개인별 선호 예측,의료, 유전자 데이터의 패턴 인식에 사용됨

from IPython.display import Image  # 주피터 노트북에 이미지 삽입

Image("C://Users/MyCom/jupyter-tutorial/kaggle/Airbnb-price-prediction/data/20211008_133615_1.png")

output_3_0

KNN 모델 테스트

import matplotlib.pyplot as plot
import numpy as np
import math

x = np.random.rand(100,1)
x = x * 10 - 5

y = np.array([math.sin(i) for i in x])
y = y + np.random.randn(100)

from sklearn.neighbors import KNeighborsRegressor

model = KNeighborsRegressor()
model.fit(x, y)

relation_square = model.score(x, y)
print('결정계수 R : ', relation_square)

y_p = model.predict(x)

plot.scatter(x, y, marker = 'x')
plot.scatter(x, y_p, marker = 'o')
plot.show()

결정계수 R :  0.5013858266279243

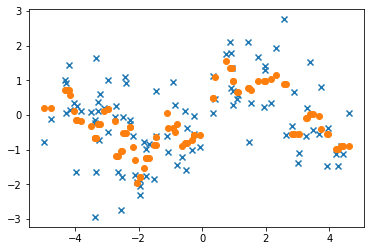
output_5_1

KNN Python 예제

총 3단계를 가지며 아래와 같습니다.

거리 계산하기
가장 근처에 있는 요소 뽑기
예측하기

# 우선 데이터 셋을 만들어 주세요

# Test distance function
# [x, y, type]
dataset = [[2.7810836,2.550537003,0],
    [1.465489372,2.362125076,0],
    [3.396561688,4.400293529,0],
    [1.38807019,1.850220317,0],
    [3.06407232,3.005305973,0],
    [7.627531214,2.759262235,1],
    [5.332441248,2.088626775,1],
    [6.922596716,1.77106367,1],
    [8.675418651,-0.242068655,1],
    [7.673756466,3.508563011,1]]

거리 계산하기

KNN의 거리를 구하는 공식은 유클리드 거리 공식을 사용합니다.

공식을 Python 함수로 나타내보겠습니다

Image("C://Users/MyCom/jupyter-tutorial/kaggle/Airbnb-price-prediction/data/20211008_134210_1.png")

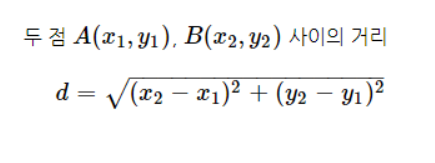
output_10_0

from math import sqrt

# calculate the Euclidean distance between two vectors
# row = [x, y, type]
def euclidean_distance(row1, row2):
    distance = 0.0
    for i in range(len(row1)-1):
        distance += (row1[i] - row2[i])**2
    return sqrt(distance)

위 함수는 유클리드 거리 공식을 사용하여 두 점사이에 거리를 구하는 공식입니다.

row에는 type까지 포함되어 있기 때문에 마지막 range는 포함하지 않고 계산합니다.

row0 = [3,3]
for row in dataset:
    distance = euclidean_distance(row0, row)
    print(distance)

2189163999999999
534510628
3965616879999998
61192981
06407232000000018
627531214
3324412480000003
922596716
675418650999999
673756466

가장 근처에 있는 요소 뽑기

# Locate the most similar neighbors
def get_neighbors(train, test_row, num_neighbors):
    distances = list()
    for train_row in train:
        dist = euclidean_distance(test_row, train_row)
        distances.append((train_row, dist))
    distances.sort(key=lambda tup: tup[1])
    neighbors = list()
    for i in range(num_neighbors):
        neighbors.append(distances[i][0])
    return neighbors

train 변수는 데이터 셋, test_row는 측정하고자 하는 좌표, num_neighbors 변수가 K를 의미 합니다.

neighbors = get_neighbors(dataset, row0, 3)
for neighbor in neighbors:
    print(neighbor)

[3.06407232, 3.005305973, 0]
[2.7810836, 2.550537003, 0]
[3.396561688, 4.400293529, 0]

예측하기

# Make a classification prediction with neighbors
def predict_classification(train, test_row, num_neighbors):
    neighbors = get_neighbors(train, test_row, num_neighbors)
    for neighbor in neighbors:
        print(neighbor)
    output_values = [row[-1] for row in neighbors]
    prediction = max(set(output_values), key=output_values.count)
    return prediction

이는 예측하는 함수로 마지막에 예측된 type을 출력해주는 함수 입니다.

# 함수를 실행하면 예측 값을 출력합니다.

row0 = [3,3,0]

prediction = predict_classification(dataset, row0, 3)
print('Expected %d, Got %d.' % (row0[-1], prediction))

[3.06407232, 3.005305973, 0]
[2.7810836, 2.550537003, 0]
[3.396561688, 4.400293529, 0]
Expected 0, Got 0.

row0 = [6,5,0]


prediction = predict_classification(dataset, row0, 3)
print('Expected %d, Got %d.' % (row0[-1], prediction))

[7.673756466, 3.508563011, 1]
[3.396561688, 4.400293529, 0]
[7.627531214, 2.759262235, 1]
Expected 0, Got 1.

가까운 type은 1이 많으므로 1로 예측하게 되죠.